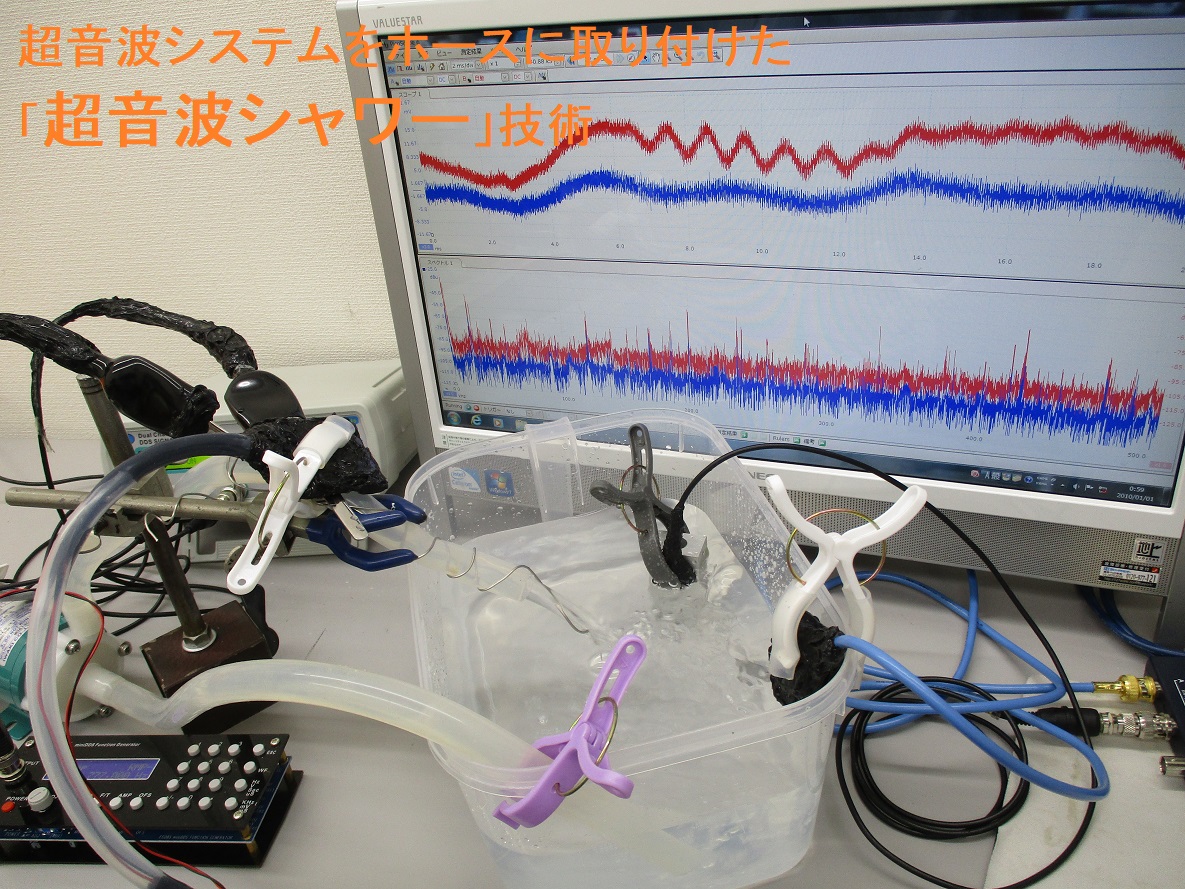
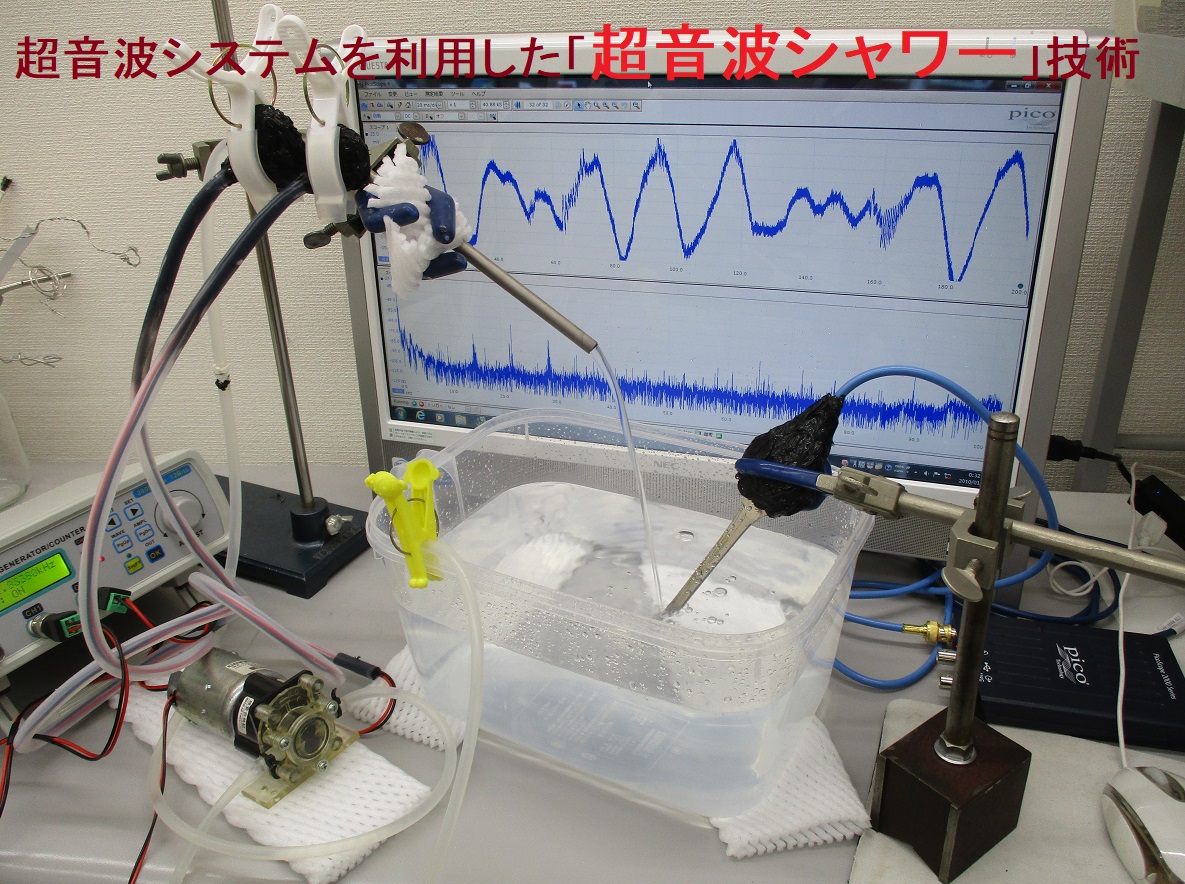
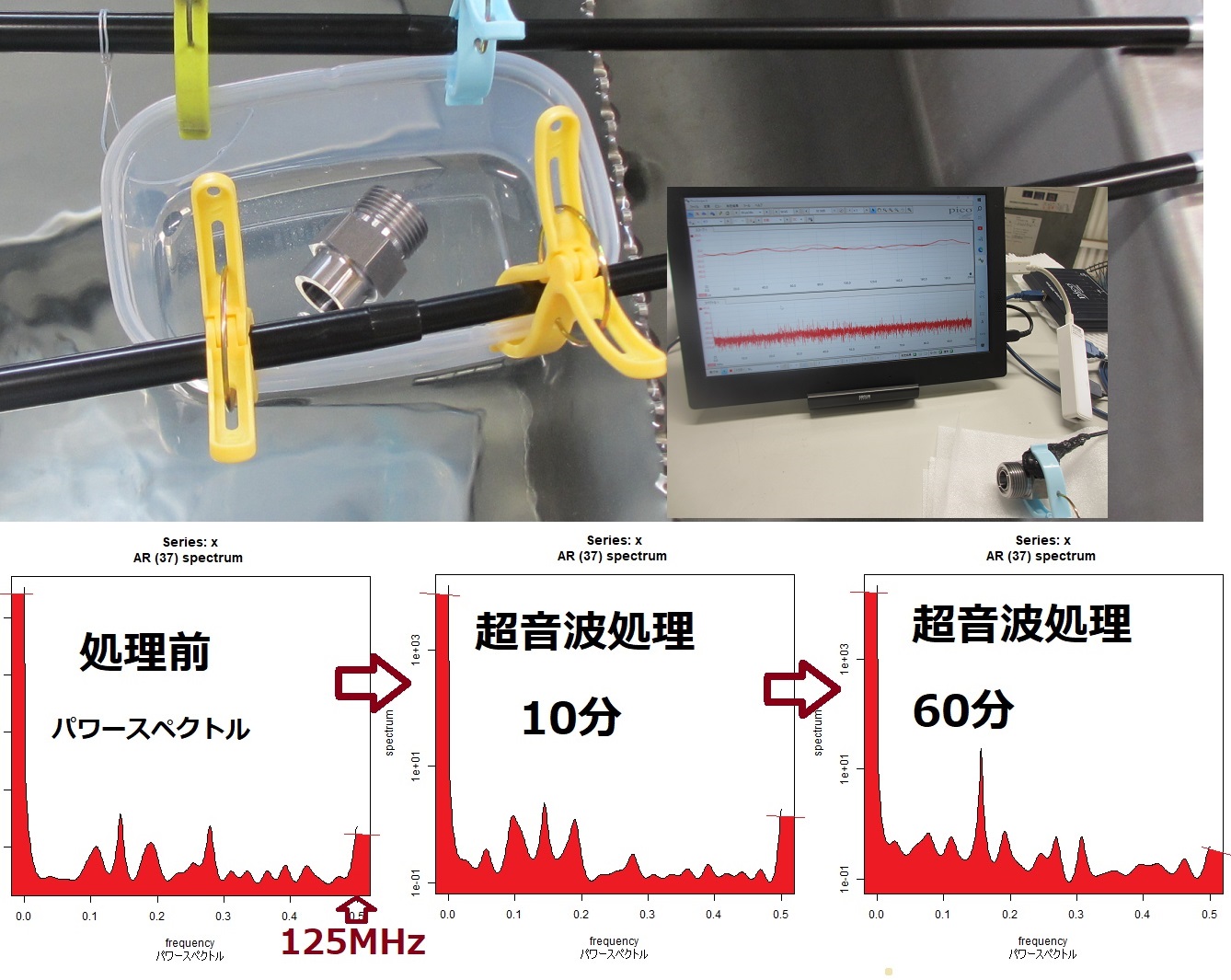
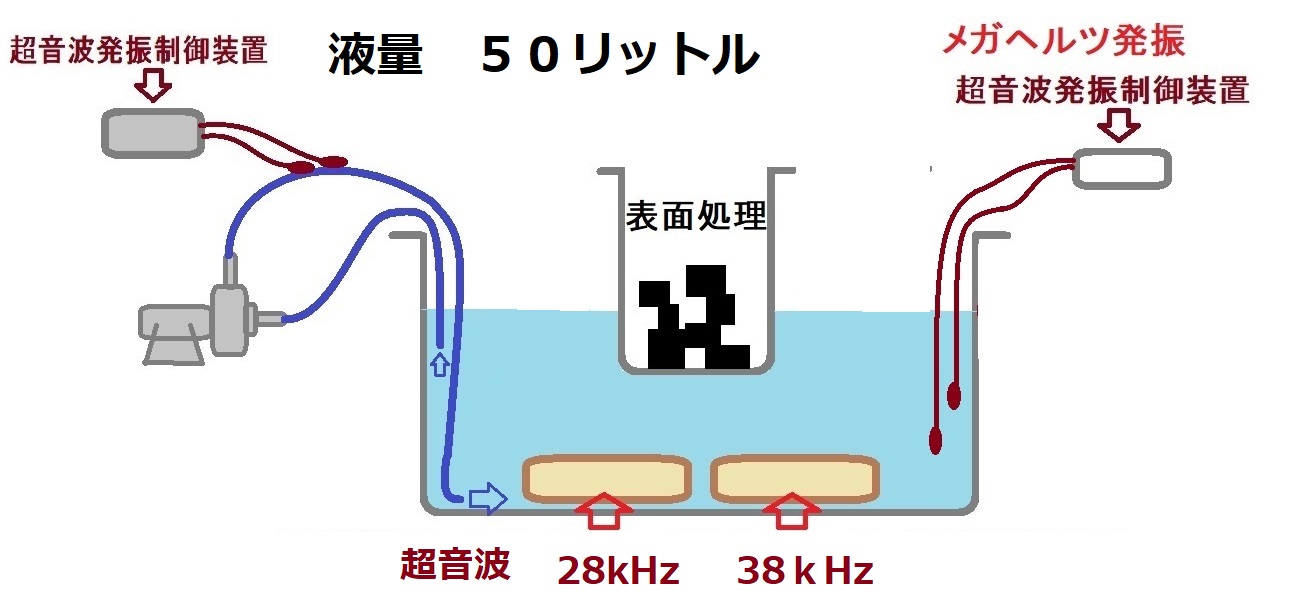
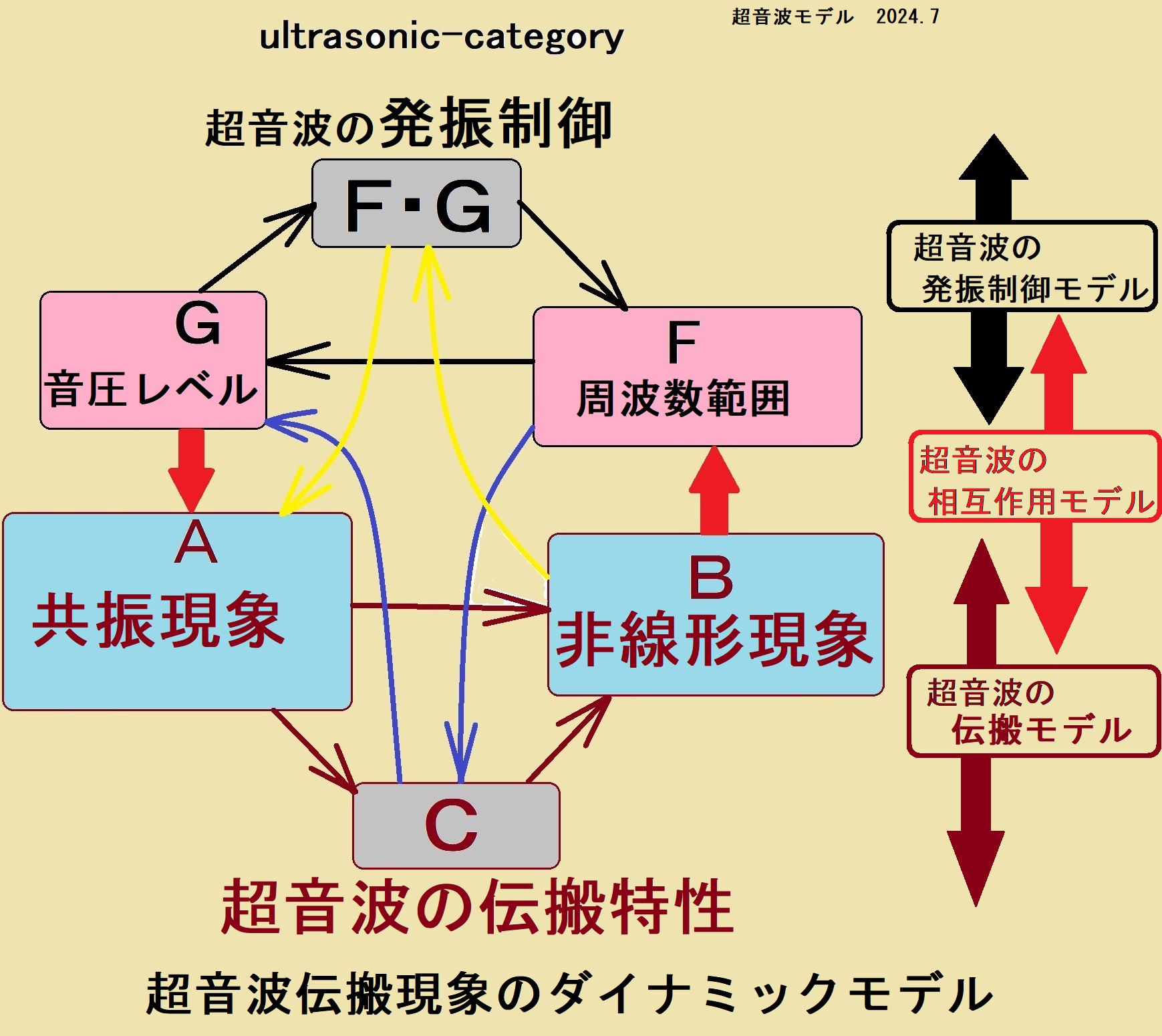
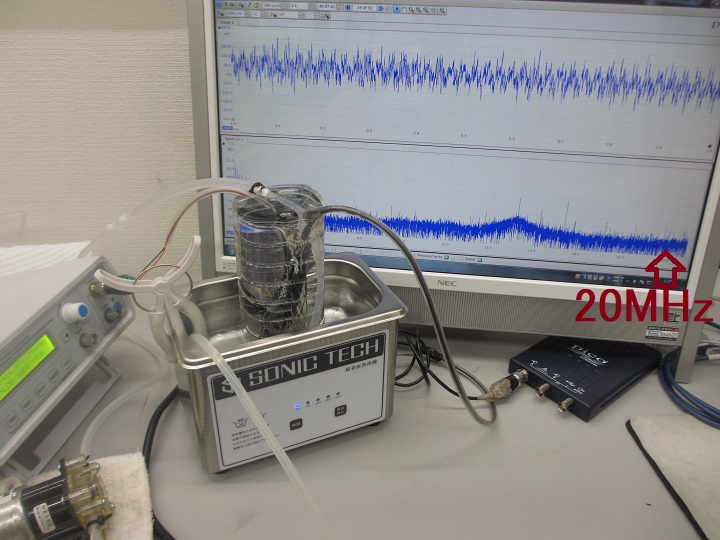
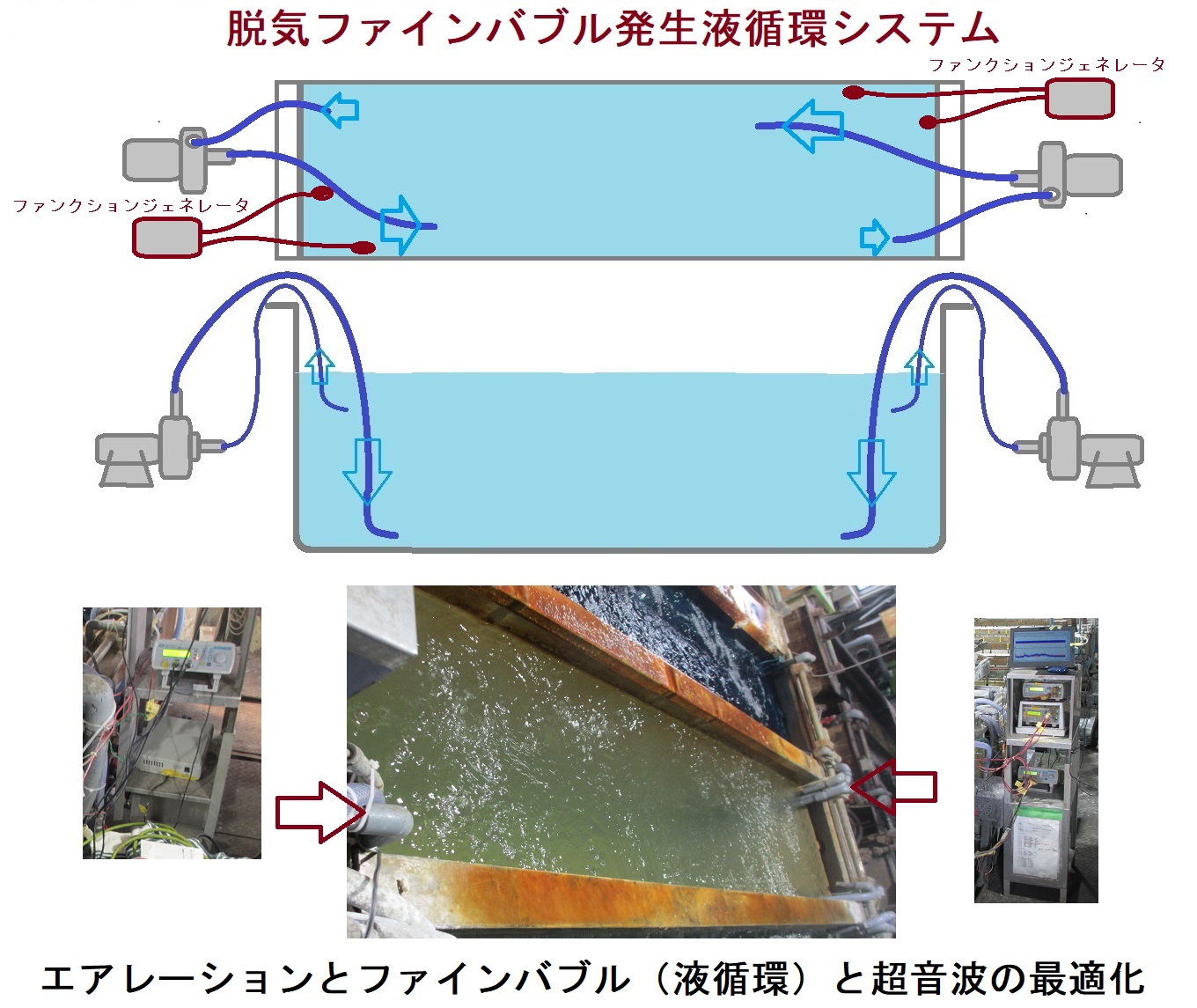
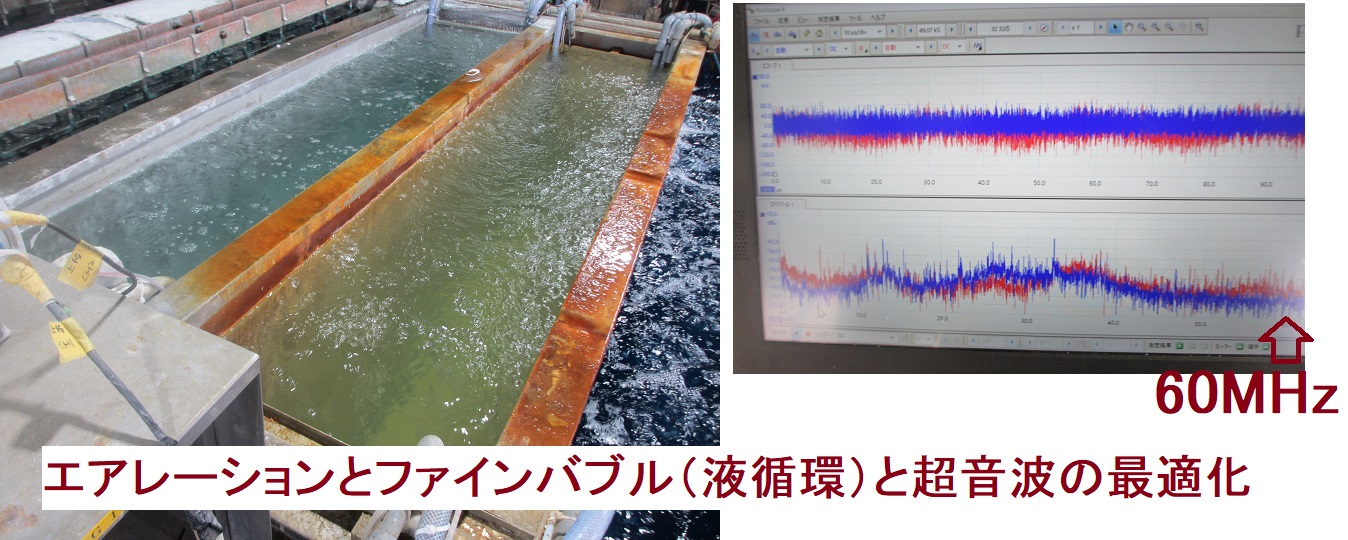
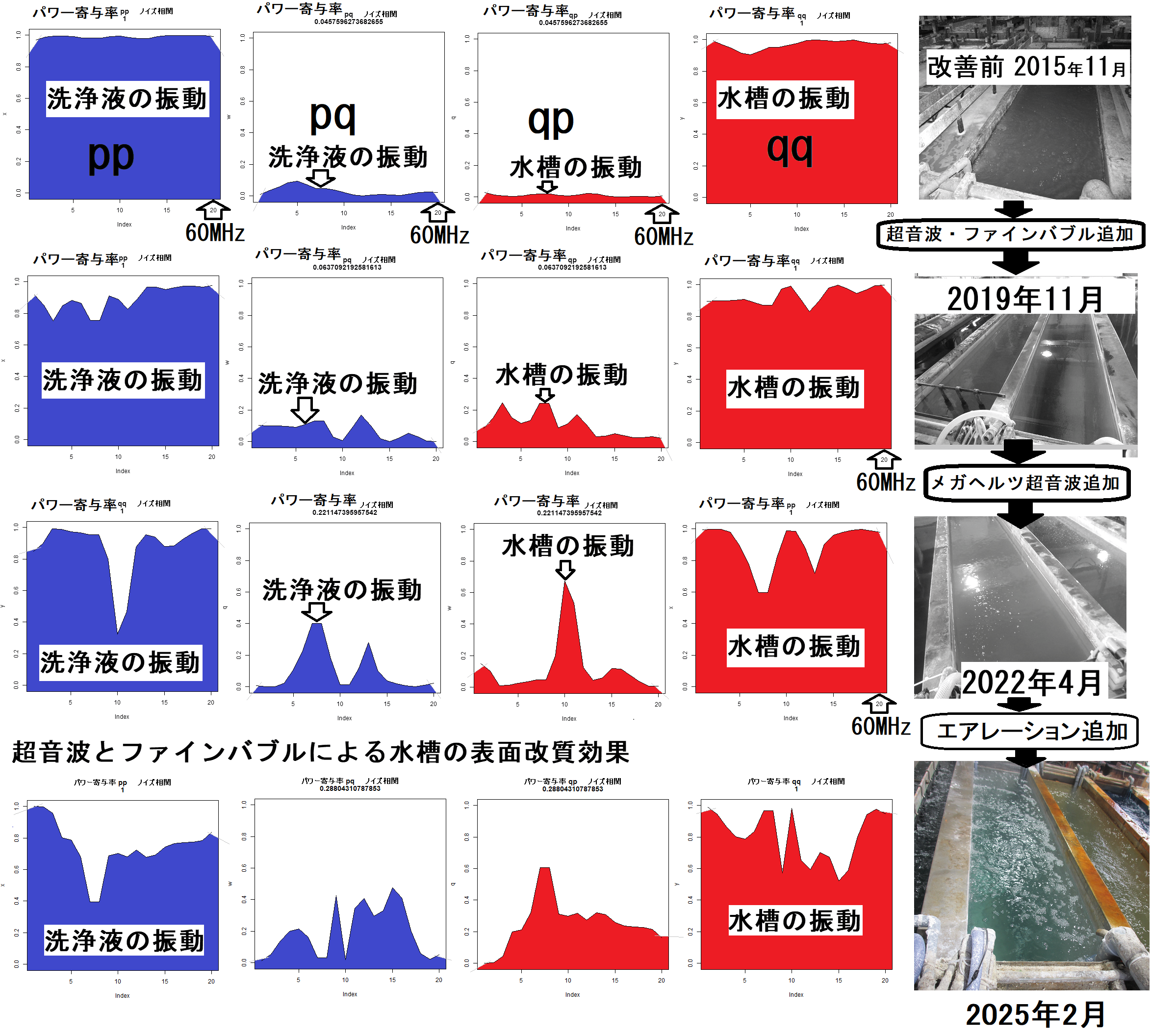
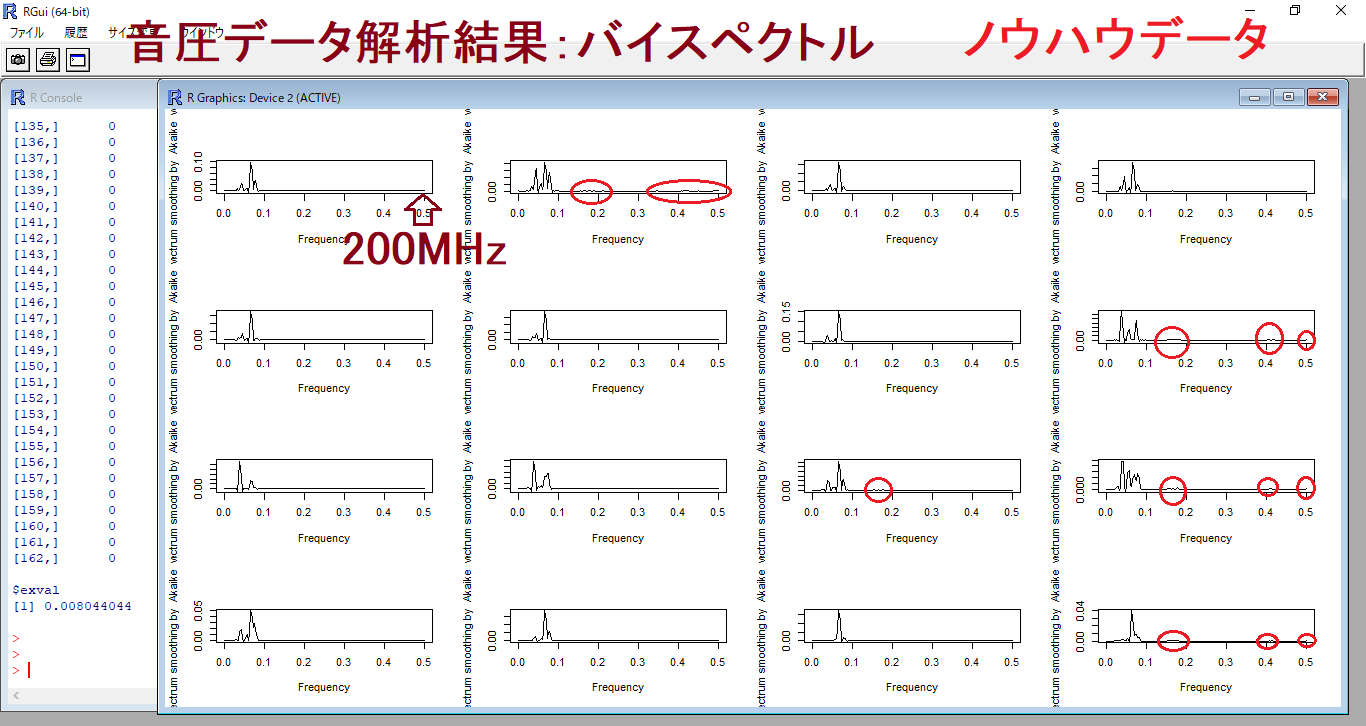
超音波システム研究所は、
超音波データのバイスペクトル解析による、
超音波伝搬現象に関する分類方法に基づいた、
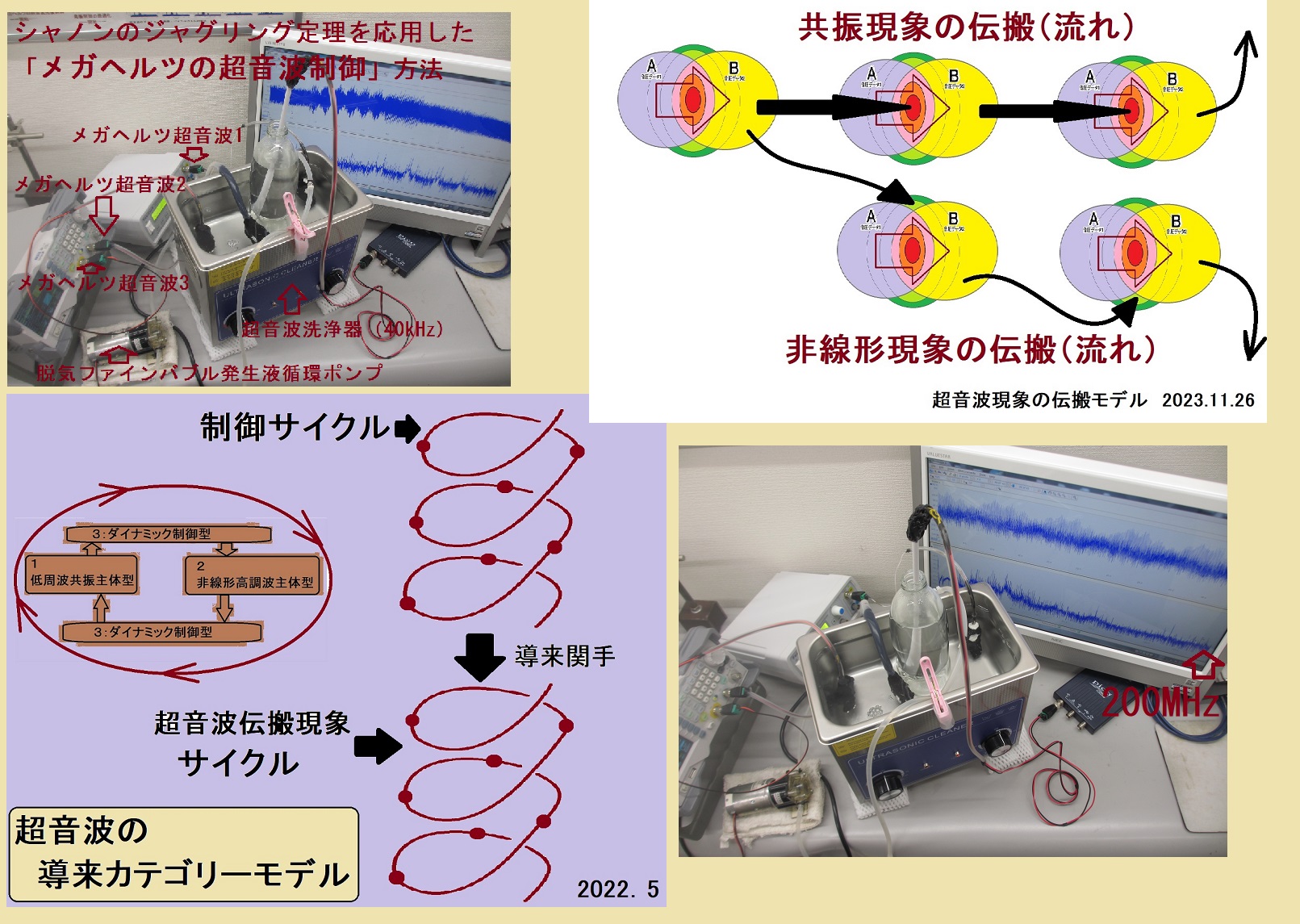
シャノンのジャグリング定理を応用した
「メガヘルツの超音波制御」方法を開発しました
この技術を、コンサルティング提案・実施対応しています。
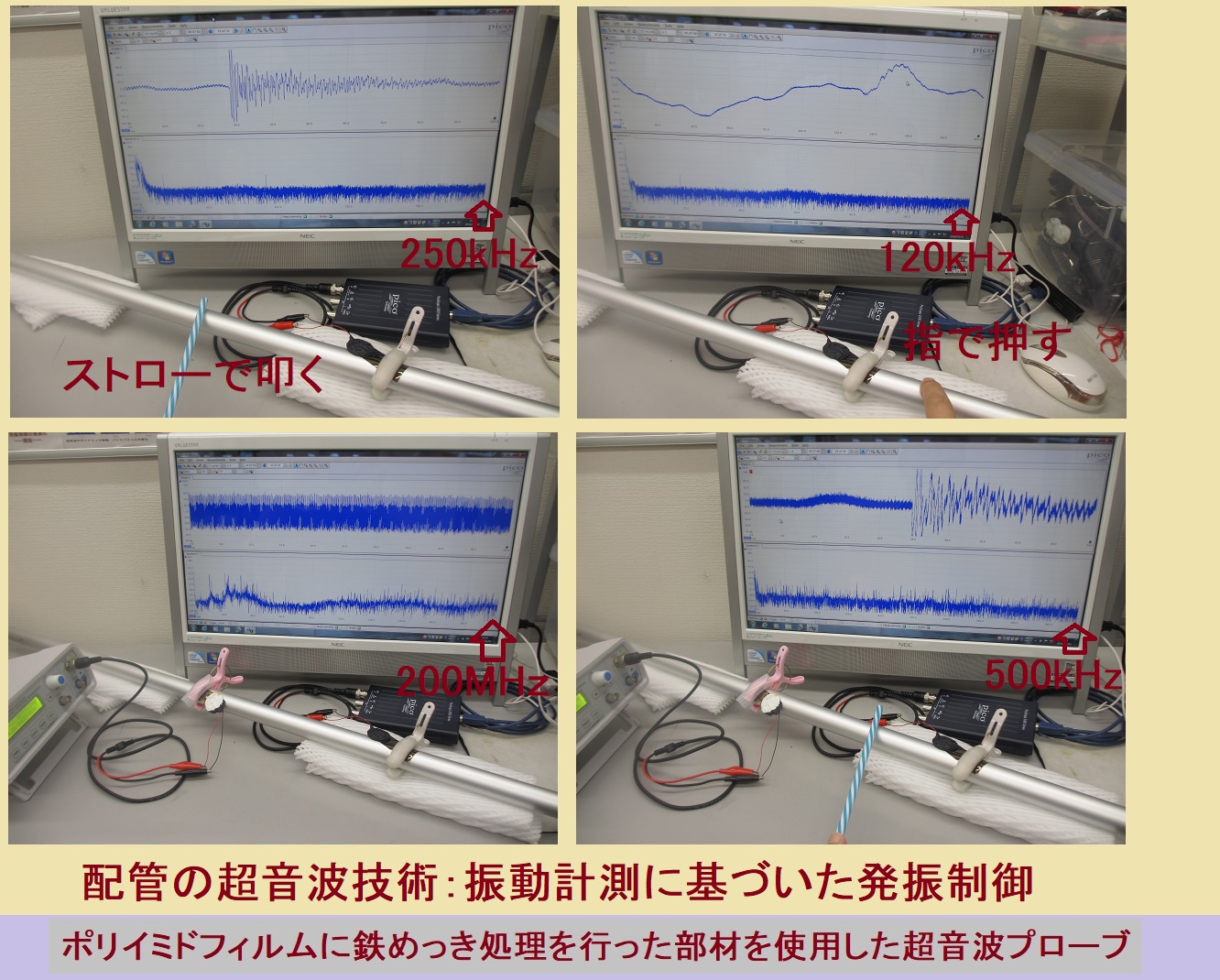
超音波伝搬現象を、安定して効率よく利用するためには
超音波の伝搬特性として、発振機や振動子以外の条件に関する
応答特性・相互作用の検討や
専用治工具の開発も必要です
発振波形や制御条件を検討することで
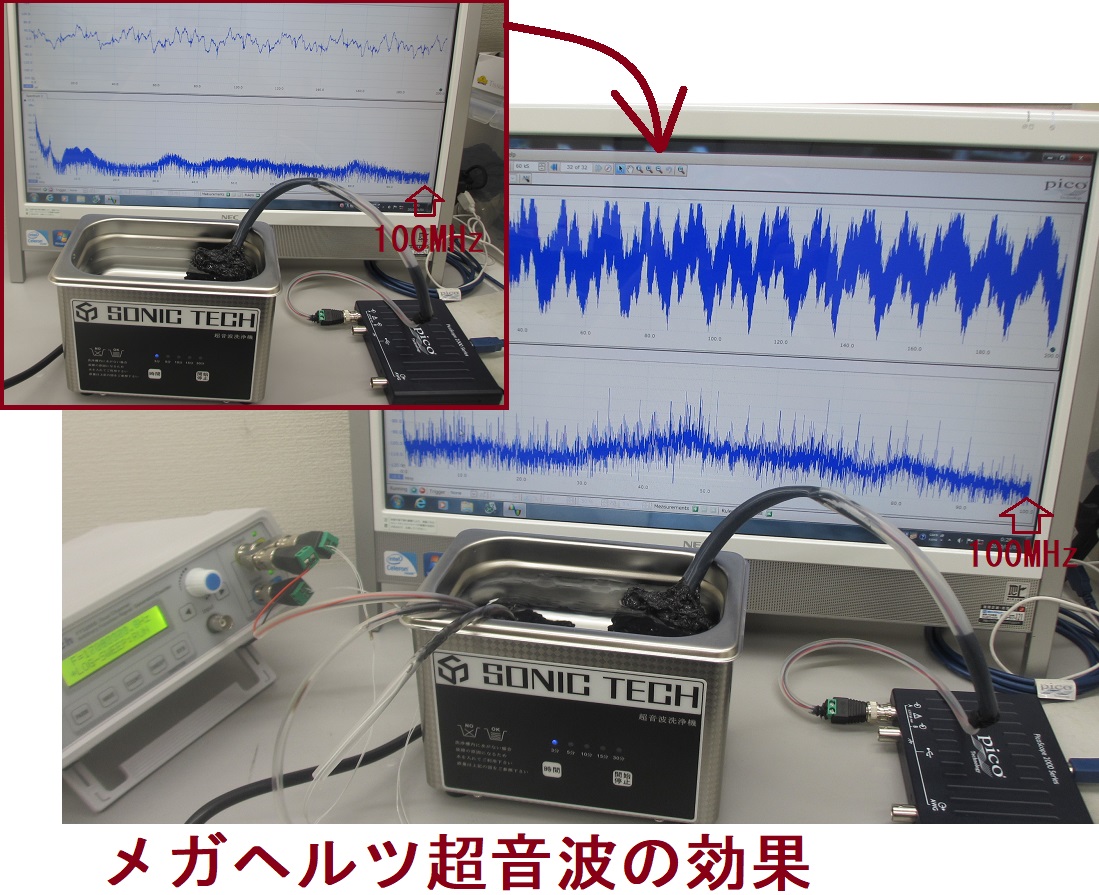
新しい超音波の効果(注1:オリジナル非線形共振現象)を発見できます
非線形現象を主要因とした、超音波現象を目的に合わせて利用することで
効率の高い超音波利用が実現します
特に、ナノレベルの超音波技術での実績が増えています
注1:オリジナル非線形共振現象
オリジナル発振制御により発生する高調波の発生を
共振現象により高い振幅に実現させたことで起こる
超音波振動の共振現象
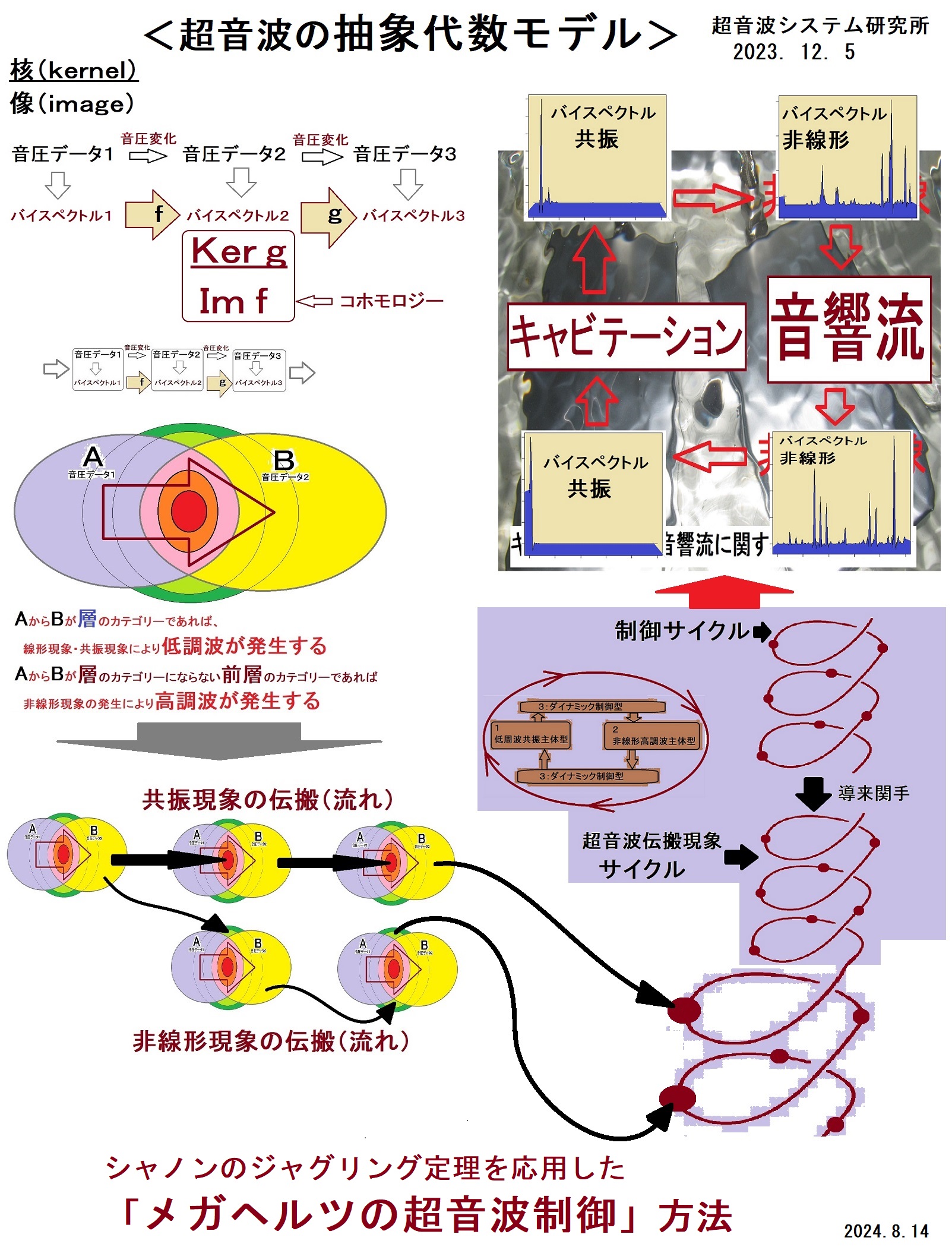
<制御について>
各種データの時系列変化の様子を解析・評価して、
時間で移動するボールのジャグリング状態に相当する
超音波伝搬現象の「サイクル」と、「影響範囲」について
超音波伝搬現象の分類(線形型、非線形型、ミックス型、変動型)から
変動型のダイナミック制御として
論理モデルを構成します
この論理モデルからボールN個のジャグリング状態を設定して制御を行い、
音圧測定解析により、非線形現象(バイスペクトル)の調整を行うと、
システムの状態に適した制御が実現し、
効率の高い超音波システムとなります
<< シャノンのジャグリング定理の応用 >>
注:JUGGLING THEOREM proposed by Claude E. Shannon
シャノンのジャグリング定理
( F + D ) * H = ( V + D ) * N
F : ボールの滞空時間(Flight time)
D : 手中にある時間(Dwelling time)
H : 手の数(Hands)
V : 手が空っぽの時間(Vacant time)
N : ボールの数(Number of balls)
<< 応用 >>
( F + F2 +・・・) * H = ( V + V2 +・・・ ) * N
F : ベースとなる超音波1の発振比率
F2 : ベースとなる超音波2の発振比率
F3 : ベースとなる超音波3の発振比率
H : 基本時間(最大制御サイクル時間)
( H=MAX(超音波1の発振サイクル、超音波2の発振サイクル・・))
V : 超音波プローブ1によるメガヘルツ発振サイクル時間
V2 : 超音波プローブ2によるメガヘルツ発振サイクル時間
V3 : 超音波プローブ3によるメガヘルツ発振サイクル時間
V4 : 超音波プローブ4によるメガヘルツ発振サイクル時間
(パルス発振の場合、サイクル時間=1)
N : 高調波の調整パラメータ 7,11,13,17,23,43,47,・・
ポイント(ノウハウ)は、非線形現象の発生状態を
音圧データの測定解析評価に基づいて、コントロールすることです。
参考動画
<<超音波の音圧測定・解析 No.2>>
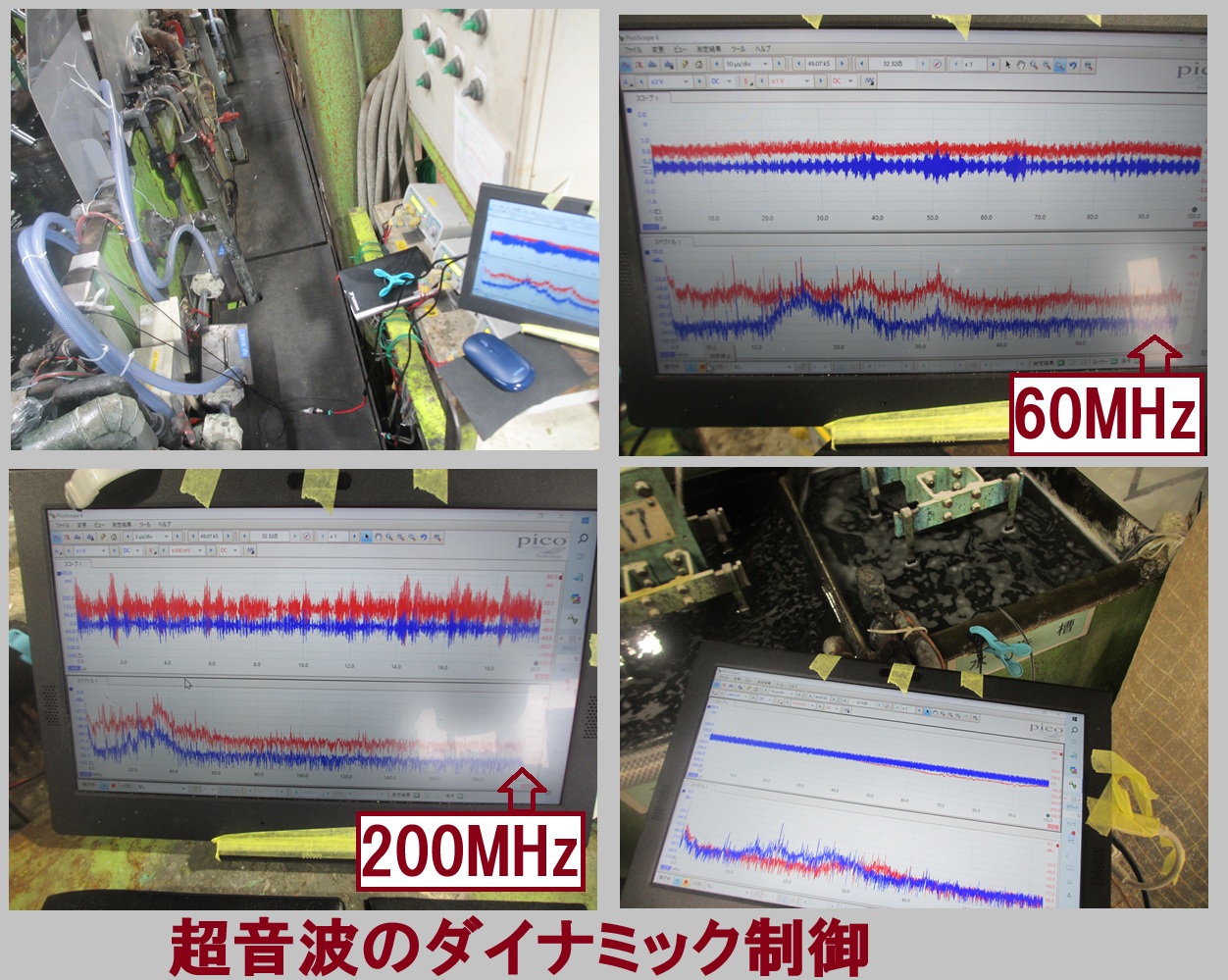
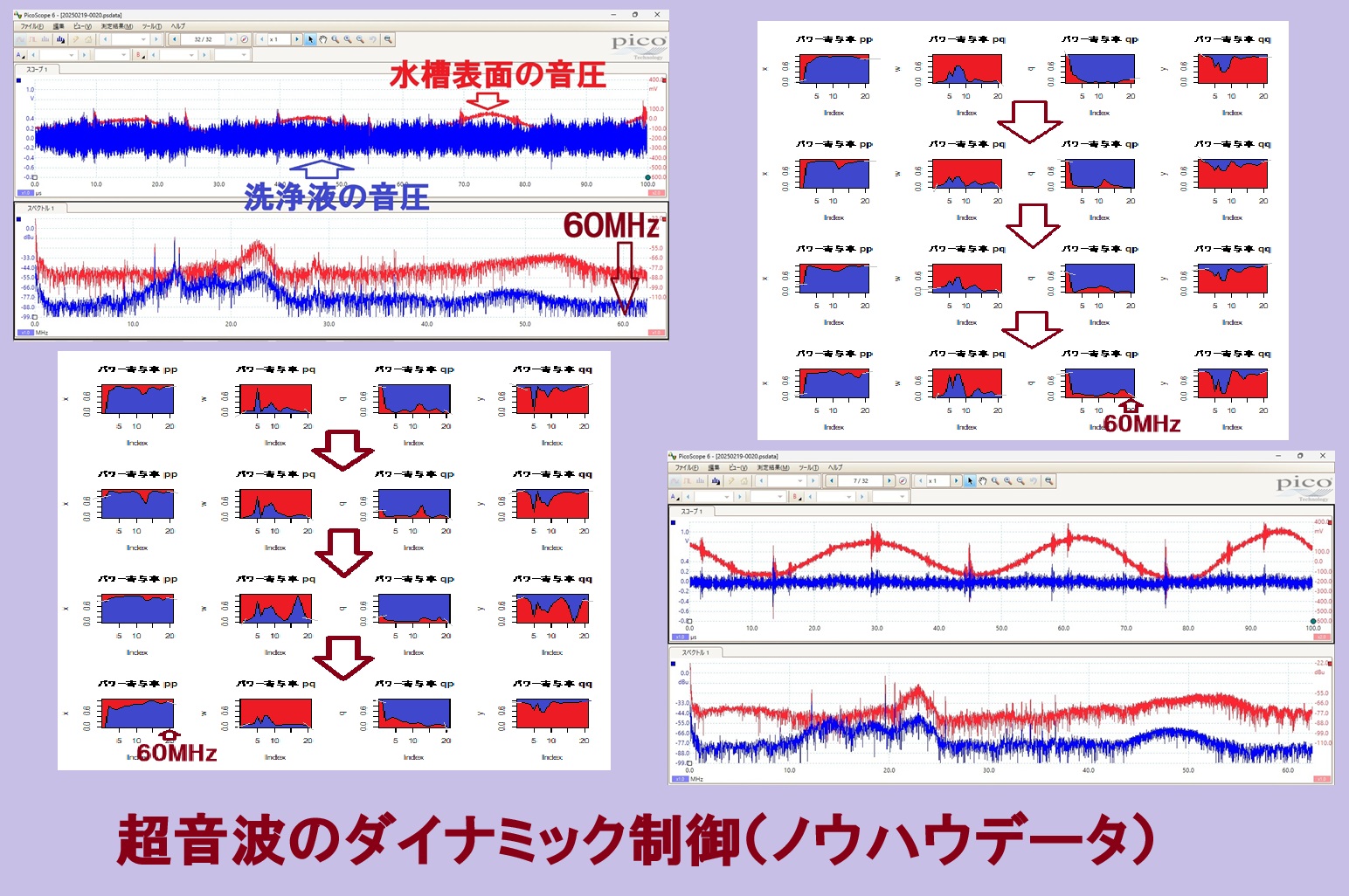
1)時系列データに関して、
多変量自己回帰モデルによるフィードバック解析により
測定データの統計的な性質(超音波の安定性・変化)について
解析評価します
2)超音波発振による、発振部が発振による影響を
インパルス応答特性・自己相関の解析により
対象物の表面状態・・に関して
超音波振動現象の相互作用として解析評価します
3)発振と対象物(洗浄物、洗浄液、水槽・・)の相互作用を
パワー寄与率の解析により評価します
4)超音波の利用(洗浄・加工・攪拌・・)に関して
超音波効果の主要因である対象物(表面弾性波の伝搬)
あるいは対象液に伝搬する超音波の
非線形(バイスペクトル解析結果)現象により
超音波のダイナミック特性を解析評価します
この解析方法は、
複雑な超音波振動のダイナミック特性を
時系列データの解析手法により、
超音波の測定データに適応させる
これまでの経験と実績に基づいて実現しています。
参考
超音波伝搬現象の分類
http://ultrasonic-labo.com/?p=10908
超音波洗浄機の「流れとかたち・コンストラクタル法則」
http://ultrasonic-labo.com/?p=17107
超音波技術:多変量自己回帰モデルによるフィードバック解析
http://ultrasonic-labo.com/?p=15785
超音波発振による相互作用
http://ultrasonic-labo.com/?p=17204
ファインバブルを利用した超音波洗浄機
http://ultrasonic-labo.com/?p=11902
超音波の音圧測定解析システム「超音波テスターNA」
http://ultrasonic-labo.com/?p=16120
超音波振動子を、超音波の利用目的に合わせて制御する方法
http://ultrasonic-labo.com/?p=9888
シャノンのジャグリング定理を応用した「超音波制御」方法
http://ultrasonic-labo.com/?p=1753
ジャグリング定理を応用した「超音波制御」方法
http://ultrasonic-labo.com/?p=19322
超音波<発振制御>技術
http://ultrasonic-labo.com/?p=5267
オリジナル超音波システムの開発技術
http://ultrasonic-labo.com/?p=1546
表面弾性波の利用技術
http://ultrasonic-labo.com/?p=7665
精密測定プローブ
http://ultrasonic-labo.com/?p=11267
「超音波の非線形現象」を利用する技術を開発
http://ultrasonic-labo.com/?p=1328
超音波<計測・解析>事例
http://ultrasonic-labo.com/?p=1705
<樹脂の音響特性>を利用した超音波システム
http://ultrasonic-labo.com/?p=7563
流れと音と形の観察:コンストラクタル法則
http://ultrasonic-labo.com/?p=7302
超音波振動子の設置方法による、超音波制御技術
http://ultrasonic-labo.com/?p=1487
超音波水槽の新しい液循環システム
http://ultrasonic-labo.com/?p=1271
超音波とマイクロバブルによる表面改質(応力緩和)技術
http://ultrasonic-labo.com/?p=5413
超音波洗浄機を改良
http://ultrasonic-labo.com/?p=1179
超音波<キャビテーション・音響流>技術
http://ultrasonic-labo.com/?p=2950
オリジナル超音波技術によるビジネス対応
http://ultrasonic-labo.com/?p=9232
超音波発振システム(1MHz、20MHz)
http://ultrasonic-labo.com/?p=18817
超音波プローブによる非線形伝搬制御技術
http://ultrasonic-labo.com/?p=9798
オリジナル超音波技術
http://ultrasonic-labo.com/?p=9894
超音波システム(音圧測定解析、発振制御)
http://ultrasonic-labo.com/?p=19422
超音波技術資料(アペルザカタログ)
http://ultrasonic-labo.com/?p=8496
メガヘルツ超音波の効果1
http://ultrasonic-labo.com/wp-content/uploads/adfb30ef89e6f5a76e9a04e70a0ca395.pdf
メガヘルツ超音波の効果2
http://ultrasonic-labo.com/wp-content/uploads/513b007f36fc8fb58a2b9c1f558d289c.pdf
表面残留応力の緩和処理技術0
http://ultrasonic-labo.com/wp-content/uploads/03bb44a2f578d71fd8d08cdc0a55a3a7.pdf
表面残留応力の緩和処理技術1
http://ultrasonic-labo.com/wp-content/uploads/9331da789c89d57b60089985daf25223.pdf
表面残留応力の緩和処理技術2
http://ultrasonic-labo.com/wp-content/uploads/21dec0bb4d122601d2edf8428a70f36d.pdf
表面残留応力の緩和処理技術3
http://ultrasonic-labo.com/wp-content/uploads/58ef187250e6b810f299dc1bf7bb0bc6.pdf